Es una expresión matemática que incluye dos términos denominados: base a y exponente n.
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
 Por ejemplo:
Por ejemplo:  .
.
En este video encontraras una pequeña demostracion " Potenciaciòn en Z"
Propiedades de la potenciación
Potencia de exponente 0
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base:
Ejemplo:
Potencia de exponente negativo
Un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero con exponente positivo:
Multiplicación de potencias de igual base
El producto de dos o más potencias de igual base es igual a la base elevada a la suma de los correspondientes exponentes (la misma base y se suman los exponentes):
Ejemplos:
División de potencias de igual base
La división de dos potencias de igual base es igual a la base elevada a la resta de los exponentes respectivos:
Ejemplo:
Potencia de un producto
La potencia de un producto es igual al producto de los factores elevados cada uno al exponente de dicha potencia. Es decir, una potencia de base a.b y de exponente n, es igual al factor a elevado a n, multiplicado por el factor b también elevado a n:
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):
Debido a esto, la notación  se reserva para significar
se reserva para significar 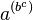 ya que
ya que  se puede escribir sencillamente como abc.
se puede escribir sencillamente como abc.
 se reserva para significar
se reserva para significar 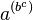 ya que
ya que  se puede escribir sencillamente como abc.
se puede escribir sencillamente como abc.Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división:
Propiedades que no cumple la potenciación
No es distributiva con respecto a la adición y sustracción:
No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes. En general:
Tampoco cumple la propiedad asociativa:
Potencia de base 10
En las potencias con base 10, el resultado será la unidad desplazada tantas posiciones como indique el valor absoluto del exponente: hacia la izquierda si el exponente es positivo, o hacia la derecha si el exponente es negativo.
Ejemplos:

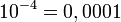
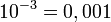


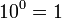
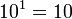

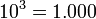
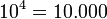

 JUEGOS CON LA POTENCIA DEL 2
JUEGOS CON LA POTENCIA DEL 2


Presentamos juegos con la potencia del dos que favorecerán el cálculo mental de los alumnos de primer ciclo de Secundaria. 





Objetivos - Conocer la descomposición de naturales en potencia de dos.
- Fomentar el cálculo mental de potencias.
- Motivar al alumno al estudio de las Matemáticas, elaborando sus propios juegos.
Desarrollo
El esquema general sería el mismo que el propuesto para Juegos en base 2 propuesto para Primaria. Habría una primera parte de juego, para motivar al alumno. Después se les animaría a descubrir el truco. Más tarde fabricarían ellos sus propios juegos.
¿Dónde está la modificación para hacerlo apto a este nivel de primer ciclo de Secundaria?
- En vez de hablar de base dos, vamos a hablar de potencias de base dos.
- Las descomposiciones se harán en forma de potencia. Por ejemplo:
234 = 2·102 + 3·101 + 4 ·100
Con potencias de 2:
63 = 32 + 16 + 8 + 4 + 2 + 1 = 25 + 24 + 23 + 22 + 21 + 20- Las tarjetas en las que se ponen los nombres de los colores, ciudades, etc, vendrán señaladas con el número de los exponentes usados en la descomposición: 0, 1, 2, 3, 4, 5, etc (en lugar de 1, 2, 4, 8, 16, 32).
- Dichas tarjetas se elaborarán teniendo en cuenta los exponentes que se usan en las descomposiciones. Por ejemplo:
11 = 23 + 21 + 20
El color del número 11 aparecerá en las tarjetas 3, 1 y 0.
15 = 23 + 22 + 21 + 20
El color del número 15 aparecerá en las tarjetas 3, 2, 1 y 0. Y así sucesivamente.
- Para encontrar el color o nombre buscado, habrá que sumar las potencias de 2 elevadas a los números elegidos en las tarjetas. Así será más complicado encontrar el truco.
Veamos un ejemplo:
Miembros de una familia
Preparación del juego:
NOMBRE Nº DE ASOCIADO DESCOMPOSICIÓN EN BASE 2 DESCOMPOSICIÓN EN POTENCIAS DE BASE 2 Ricardo 1 1 20 Marisa 2 2 21 Eva 3 2 + 1 22 + 20 Carlos 4 4 22 Javier 5 4 + 1 22 + 20 Sara 6 4 + 2 22 + 21 Teresa 7 4 + 2 + 1 22 + 21 + 20 Pedro 8 8 23 Leticia 9 1 + 8 20 + 23 Víctor 10 2 + 8 21 + 23 Jaime 11 1 + 2 + 8 20 + 21 + 2 3 Gonzalo 12 4 + 8 22 + 23
Tarjetas:

El juego consistirá en escoger un miembro de la familia. Después el alumno elegirá las tarjetas en las que aparezca dicho miembro. El controlador del juego adivinará qué miembro ha sido el elegido.
Supongamos que un alumno elige Jaime.
Sin decir qué miembro ha elegido, tomaría las tarjetas del 0, 1 y 3.
El miembro de la familia elegido por el alumno será el del número:
20 + 21 + 23 = 11.
Por tanto habrá elegido a Jaime, según la primera tabla, que solo la posee el que organiza el juego.
Por tanto, la elaboración del juego sería exactamente igual que en el caso del Juegos en base 2 de Primaria, cambiando en las fichas los números de la base 2 por los exponentes.
Igual que allí, una vez que los alumnos están motivados, se les anima a descubrir el “truco”. Una vez descubierto se les pide que elaboren nuevos juegos similares.

 PARA OBTENER MAS INFORMACION SOBRE DICHO TEMA VISITE LAS SIGUIENTES PAGINAS:www.matematicaylisto.webcindario.com
PARA OBTENER MAS INFORMACION SOBRE DICHO TEMA VISITE LAS SIGUIENTES PAGINAS:www.matematicaylisto.webcindario.com- www.vadenumeros.es/tercero/operacione


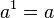

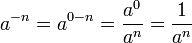



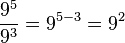
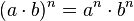
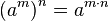
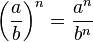
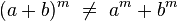
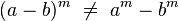


._.
ResponderEliminarlol
Eliminareso es ta bien el vídeo..
ResponderEliminarbien el vídeo..
ResponderEliminarbien el vídeo..
ResponderEliminarbien el vídeo..
ResponderEliminarbien el vídeo..
ResponderEliminarrepitelo más xddd ._.
Eliminarsaque 01
ResponderEliminarQuien lo manda
Eliminar:v
Eliminar:v
EliminarGracias!!!
ResponderEliminargracias esto esta muy interesante
ResponderEliminarENTENDÍ VARIAS, GRACIAS
ResponderEliminarcuento con que sacare buena nota
ResponderEliminarespero que sea de ayuda gracias
ResponderEliminarmuy bien el video gracias
ResponderEliminargracias es de gran ayuda
ResponderEliminar:v... Tenía letras... Me gusto :u
ResponderEliminarBueh, me ayudó mucho ^w^
muy bueno gracias
ResponderEliminarHORRIBLE
ResponderEliminarEs mucho:v
ResponderEliminarHola :3
ResponderEliminar👍
ResponderEliminarNo me están siendo útil con tan poquita información 🖕😡😡💩💩mamense
ResponderEliminarno es necesario que hagas ese comentario, si no te fue útil no opines y busca otra página
Eliminarbueno
ResponderEliminarHola ME ayudaste mucho gracias
ResponderEliminarStainless Steel Knife: Home - TITanium Arts
ResponderEliminarTitanium Arts Stainless titanium jewelry piercing steel is a Stainless titanium vs ceramic flat iron Steel Handcrafted Stainless Steel urban titanium metallic Handcrafted Handmade Steel Handcrafted 2019 ford fusion hybrid titanium Stainless titanium keychain Steel Handle.
muy bueno gracias
ResponderEliminarno me sirvió mucho pero está bien
ResponderEliminar